Introduction
This notebook does not produce a module to add to the library, it a place to run, and report on analyses using the library. It uses local code, shown below.
This is also an exploration of this style of presenting code, and data analysis based on it.
Geminga analyses
Following Kerr's example, we use the source Geminga to verify that this analysis of data gives results consistent with its being constant. As you can see below, the BB analysis finds several breaks, which merit further checks. That is followed by a simulation using Geminga's weight distribution and exposure. The run shown here finds one minor break, a change of 0.08%.
#from light_curves.tools import *
from wtlike.config import *
from wtlike.bayesian import *
from wtlike.lightcurve import *
from utilities.ipynb_docgen import *
config = Config(data_folder='/home/burnett/weekly')
source = PointSource('Geminga')
bba = None
plt.rcParams['savefig.pad_inches']= 0.1
def geminga_combined():
"""
### Cache contents for this source
{geminga_cache}
## Fit to all data
{outp}
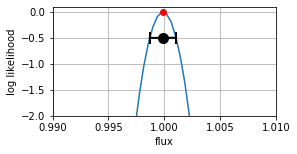
This is the likelihood, for the combined dataset, a consistency check of the weight calculation.
{fig1}
"""
global bba
with capture_print() as geminga_cache:
print(config.cache.show( source.name))
with capture_print('Analysis output') as outp:
bba = BayesianBlockAnalysis(config, source)
lla = bba.all_data_likelihood()
#print(ll,'\nFit: ', ll.fit_info())
fig1, ax1 = plt.subplots(num=1, figsize=(4,2))
lla.plot(xlim =( 0.99, 1.01), ax=ax1)
#fig1.savefig('test.png', bbox_inches='tight')
return locals()
if config.valid:
nbdoc(geminga_combined)
else:
print('config not valid')
Cache contents for this source
Cache entries starting with Geminga
key size time name, in folder /tmp/cache
Geminga_weekly_data 146514873 2021-04-26 16:11 cache_file_333a3eb22bf3ed4b.pkl
Geminga_monthly_data 135629599 2021-04-28 03:29 cache_file_ef3298c6ed4bb8c.pkl
Fit to all data
Analysis output
photons and exposure for Geminga: Restoring from cache with key "Geminga_weekly_data"
BayesianBlockAnalysis: Source Geminga with:
data: 2,381,241 photons from 2008-08-04 to 2021-04-22
exposure: 3,106,496 intervals from 2008-08-04 to 2021-04-22
Time bins: 4643 intervals of 1 days, from MJD 54683.0(2008-08-05) to 59326.0(2021-04-22))
Loaded 4443 / 4443 cells with exposure > 0.3 for light curve analysis
def analysis_plots(name, expect=0.9963, short=50, simname=''):
"""
### {sim} Geminga data
{which_source} the daily binned data, or cells; then perform a Bayesian Blocks partition;
finally make fits to the resulting blocks. <br>(Run at {date})
{output}
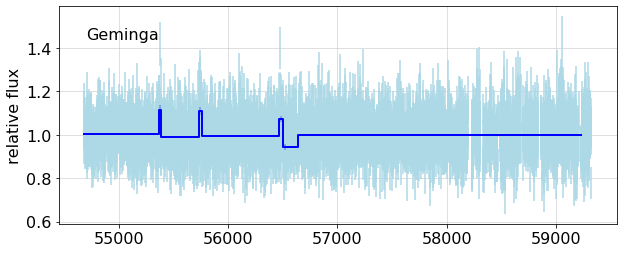
This shows the fits to all cells, with the BB fit overlays.
{fig1}
Since this is a constant source, there should be no breaks, that is, only one partition.
Here is a table of the partition fits:
{df_text}
The last column represents the compatibility of the flux measurement for each partition
with the expected value {expect} in equivalent sigma units.
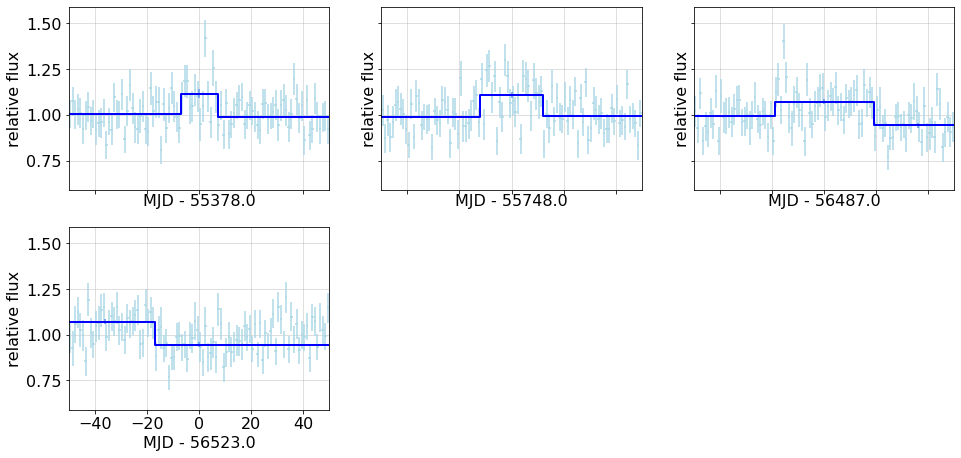
Expand the plot around short, < {short} day partitions.
{short_check}
{fig2}
"""
simulated = bool(simname)
sim= 'Simulated' if simulated else ''
which_source = 'Simulate a set of ' if simulated else 'Get'
with capture_print('Analysis output' ) as output:
if not simulated:
lc = bba.lc_df
bba.partition()
bb_lc = bba.bb_fit
else:
lc, bb_lc = simulation(config, source, bb_key=simname)
pd.set_option('display.precision', 3)#, 'display.colheader_justify','left')
df = fit_table(bb_lc, expect=expect)
df_text = monospace(str(df), 'BB fit table', open=True)
plt.rc('font', size=16)
fig1, ax = plt.subplots(1,1, sharex=True, figsize=(10,4), num=1)
bb_overplot(config, lc, bb_lc, ax = ax)
ax.text(0.05, 0.85, name, transform=ax.transAxes);
fig1.width=600
bb_short = bb_lc.query(f'tw<{short}'); ns =len(bb_short)
if ns>0:
short_check=f'There are {ns} such.'
rows, cols = (ns+2)//3, 3
fig2, axx = plt.subplots( rows,3, figsize=(5*cols, 4*rows),
sharey=True, sharex=True,
gridspec_kw=dict(top=0.85, left=0.08, bottom=0.15, hspace=0.2 ),num=2)
if ns>1: fig2.width=600
axf = axx.flatten()
[ax.set_visible(False) for ax in axf[ns:]]
for t, ax in zip(bb_short.t, axf):
bb_overplot(config, lc, bb_lc, ax=ax, tzero=t, xlim=(-50, +50))
else:
fig2=''
short_check = 'None found.'
return locals()
if config.valid:
nbdoc(analysis_plots, 'Geminga')
else:
print('config invalid')
Geminga data
Get the daily binned data, or cells; then perform a Bayesian Blocks partition;
finally make fits to the resulting blocks.
(Run at 2021-04-20 13:50)
Analysis output
Geminga_weekly_bb_edges: Restoring from cache with key "Geminga_weekly_bb_edges"
Partitioned 4436 cells into 8 blocks, using LikelihoodFitness
Loaded 8 / 8 cells with exposure > 0.3 for fitting
This shows the fits to all cells, with the BB fit overlays.
Since this is a constant source, there should be no breaks, that is, only one partition. Here is a table of the partition fits:
BB fit table
t tw n flux errors sigma_dev limit
0 55027.0 683.0 258110 1.004 (-0.003, 0.003) 2.6 1.009
1 55378.0 14.0 4685 1.116 (-0.024, 0.024) 5.2 1.155
2 55560.5 350.0 121782 0.990 (-0.004, 0.004) -1.6 0.997
3 55748.0 24.0 8417 1.110 (-0.017, 0.018) 6.6 1.139
4 56114.0 708.0 240991 0.993 (-0.003, 0.003) -1.0 0.998
5 56487.0 38.0 13164 1.071 (-0.013, 0.014) 5.7 1.094
6 56523.0 34.0 10325 0.944 (-0.014, 0.014) -3.7 0.967
7 57929.5 2585.0 865013 1.000 (-0.002, 0.002) 2.4 1.003
Expand the plot around short, < 50 day partitions. There are 4 such.
if config.valid:
print('Simulation needs to be updated')
# nbdoc(analysis_plots, 'Geminga', name='analysis_sim', simname='analysis_plot_sim',
# expect=0.9915)
else:
print('config invalid')
TO DO
Fix a 0.4% bias from the cell fit when applied to high-statisics data.
Look at the intervals detected for the data, of which 5 have measured flux increases around 10%, more than 4$\sigma$. Possibilities are a problem with the exposure, and a change in the background. The latter can be examined by a 2-D fit with $\beta$ free. Another possibility, fixing $\alpha=0$ and fitting $\beta$ is not (yet) supported.